Finally, I’m on the last of the exercises from Chapter 2 of A Programmer’s Introduction to Mathematics. The exercise prompts are deceptively terse, and their connection to the material presented in the chapter is not always immediately obvious. Working through them can take entire days (for me, anyway).

Write a web app that implements the distribution and reconstruction of the secret sharing protocol using the polynomial interpolation algorithm presented in this chapter, using modular arithmetic modulo and a 32-bit modulus \(p\).

To be honest, it took many hours before I could even understand what I was actually being asked to do. I understood

• part of the what: the concept of modulo, and
• the why: modular arithmetic avoids floating-point rounding errors that emerge in the \(\frac{x - x_j}{x_i - x_j}\) operation of interpolating polynomials

But I was clueless about the rest—namely

• how modular arithmetic relates to polynomials; do you perform \(\mod n\) on all the coefficients?
• how does division (fractional quantities) even work in modular arithmetic?

At first, I spent way too much time going down fruitless dead-ends. I tried adding in mod in random places, but I still got floating-point rounding errors.

Multiplicative inverse

Eventually, I found my way to the key insight that got things moving: There is no “division” as such in modular arithmetic. Instead, there is the multiplicative inverse, which is analogous in a somewhat non-obvious way to regular division.

In normal arithmetic, the inverse of a number (let’s say \(b\)) is the entity that, when multiplied by \(b\), gives \(1\). That will be the reciprocal, and if \(b\) is a whole number, then the inverse of \(b\) can be written \(b^{-1}\).

In modular arithmetic, the multiplicative inverse of a number \(b\) in \(\mod n\) is also written \(b^{-1}\), and it is the integer that, when multiplied by \(b\), gives \(1 \mod n\):

Now, finding the inverse is not exactly straightforward. There is an algorithm, but let’s first explore some examples. The StackExchange answer linked above enumerates the multiplicative inverses of numbers in \(\mod 11\):

Back to division. In normal arithmetic, we can use the property of the inverse to rewrite fractions in a slightly awkward way: \(\frac{a}{b} = a \cdot \frac{1}{b} = a \cdot b^{-1}\).

By this logic, “division” can be performed in modular arithmetic by multiplying \(a \cdot b^{-1} \mod n\) and reducing the answer you get \(\mod n\). For example, \(\frac{7}{6}\) would be obtained in \(\mod 11\) by:

Interestingly, for prime moduli, there is a very quick and easy way to do it natively in Python, which is much faster and simpler than the full algorithm for arbitrary moduli:

def mod_inv(x, mod):
    return pow(x, mod-2, mod) # Same as x ** mod-2 % mod

mod_inv(6, 11) # 2

I don’t really understand the -2 part, but it seems that in \(\mod 11\), any number raised to the ninth power will produce a number that is one more than a multiple of 11.

Polynomial interpolation, modularly

Now, to apply this finding to polynomial interpolation. This was the original, non-modular, non-cool version:

To make it modular and cool, we do this:

Keeping in mind that the equivlent of modular a / b in Python is a * mod_inv(b, mod) % mod, this is surprisingly easy to implement in the author’s single_term function (original code is here). Let’s assume a global variable MOD that we’ll create later.

theTerm = theTerm * Polynomial([-xj / (xi - xj),
                                1.0 / (xi - xj)])

theTerm = theTerm * Polynomial([-xj * mod_inv(xi - xj, MOD) % MOD,
                                mod_inv(xi - xj, MOD) % MOD])

The coefficients of the polynomial generated by the interpolate function must also be reduced. Code-wise, that’s pretty easy:

return sum(terms, ZERO)

return sum(terms, ZERO) % MOD

Except for one thing—the original class made no provision for the % operator. So we have to add that to the class (original code is here):

def __mod__(self, other):
    self.coefficients = [c % other for c in self.coefficients]
    return self

Finally, the value returned by evaluateAt must also be reduced \(\mod n\):

return theSum

return theSum % MOD

For some reason, the ZERO polynomial has to be changed slightly:

ZERO = Polynomial([])

ZERO = Polynomial([0])

Making floating points sink

Modular arithmetic only deals with integers, or int, so care must be taken to avoid any accidental coercion to floats in the course of the code. Otherwise, that defeats the purpose of going through all this trouble to avoid floating-point rounding errors.

The initial value of each single term in the single_term function is a float, so let’s change that:

theTerm = Polynomial([1.])

theTerm = Polynomial([1])

Summing a list of Polynomials (or even just adding two together) produced floating-point values even when the original coefficients were integers. It turns out that the author explicitly coerced the value in the function add of the Polynomial class (which was loaded into the operator via __add__). Another easy fix:

sum(x) for x in zip_longest(self, other, fillvalue=0.)

sum(x) for x in zip_longest(self, other, fillvalue=0)

Modulus Prime

Man, the word modulus is such a cool word. Anyway, we need to create one.

The prompt in the book specifies the use of a 32-bit number. It just so happens that Python has a handy random number generator, random.getrandbits(32), that takes x bits as an argument.

Since our simplified algorithm for modular exponentiation assumes that the modulus is prime, we also have to find some way to check for primality. sympy has one such function; no need to reinvent the wheel. (While I am finding number theory very fascinating, I also don’t have 5 years to spend on one chapter of this book!)

So, with that information, it should be pretty easy to come up with a random 32-bit prime modulus:

import random
from sympy.ntheory.primetest import isprime

random.seed(2)

def big_prime():
    while True:
        p = random.getrandbits(32) # a random 32-bit number
        if isprime(p):
            break
    return p

MOD = big_prime()

This instantly gives us gigantic numbers like 3898342621 that automatically satisfy two conditions: (1) Occupy 32 bits and (2) Be prime. Perfect!

The proof is in the polynomials

MOD # 2606193617
points = [(1, 5), (2, 6), (7, 7)]
f = interpolate(points) # 347492486 + 2084954895 x^1 + 173746241 x^2
[f(xi) for (xi, yi) in points] # [5, 6, 7]

It works! Our interpolated polynomial is

and despite the enormous coefficients, it does actually pass through the points I specified.

It should be noted that this code does not work for negative numbers, as someone commented in response to the quick-and-dirty modular exponentation function I found on Stack Exchange. You can make modular arithmetic work with negative numbers, but it takes a little more fiddling.

You could also just take the lazy route and not use negative \(y\) values when implementing this for secret-sharing.

Just out of curiosity, what does this modular polynomial look like, compared to the non-modular one?

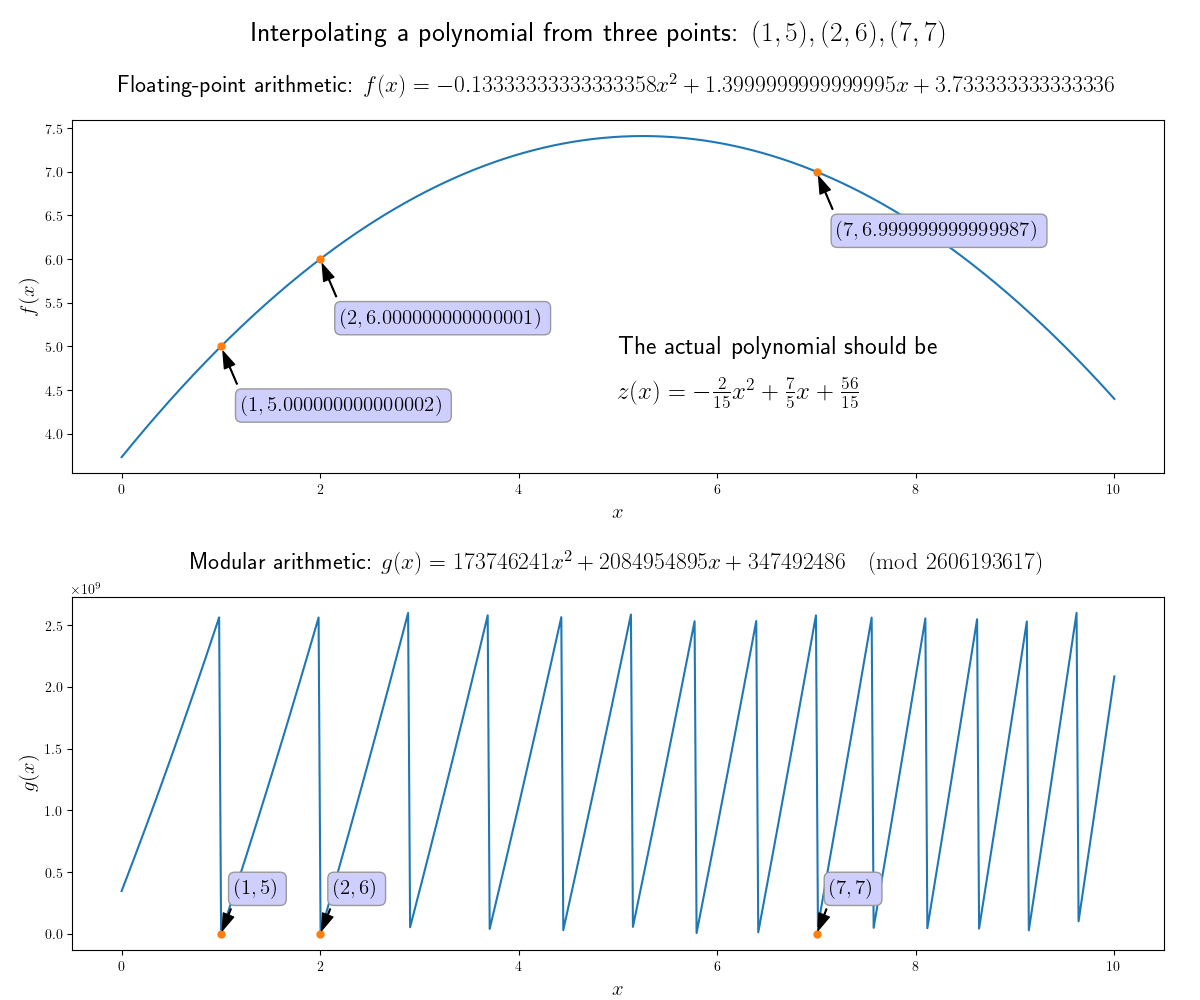
The modular polynomial has an interesting shape! Note that the scale on the vertical axis is 1e9, or one billion.

I find it so bizarre and fascinating that the floating-point coefficients are off by such a small amount, yet result in an inaccuracy that would make the result completely useless for cryptography, while the modular coefficients are so gigantic (along with the fluctuations in the graph) yet do create a polynomial that passes through the given points.

To illustrate just how small the floating-point errors are, here is a comparison between the floating-point and decimal version of the hand-interpolated polynomial:

That’s enough for this post. I’ll get on implementing this into an actual toy-cryptography web app soon!

References

• How to compute \(\prod_{i=1}^n y'{_i}^{\big(\prod_{j \not=i, j=1}^n \frac{x_j}{x_j-x_i}\big)}\) with modular arithmetic for Lagrange, Stack Exchange Mathematics
• Modular multiplicative inverse function in Python, Stack Overflow

// filed under modular arithmetic in Math    // share on Twitter